The Fundamental Theorem of Calculus
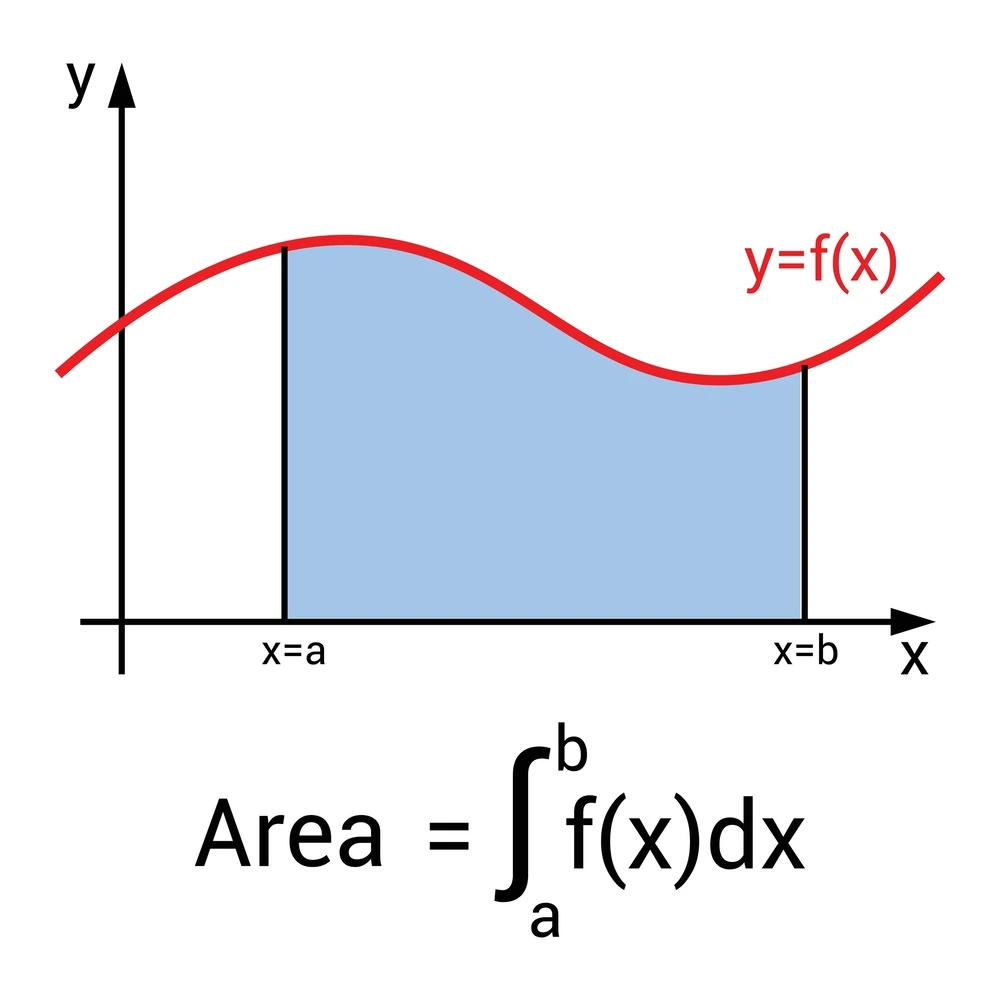
In calculus, integration is the process of calculating integrals. While derivatives are used to find the rate of change of a function, a definite integral evaluates the exact accumulation of quantities. Most commonly, it represents the exact signed area defined by the region plotted on a graph between a given mathematical curve and the horizontal x-axis.
The Fundamental Theorem of Calculus acts as the critical bridge connecting differentiation and integration. It states that if a function \( f(x) \) is continuous over an interval \( [a, b] \), and \( F(x) \) is its antiderivative, then the definite integral can be evaluated precisely by subtracting the value of the antiderivative at the lower limit from the antiderivative at the upper limit: \( \int_{a}^{b} f(x) dx = F(b) - F(a) \).
Indefinite vs. Definite Integrals
It is vital to understand the distinction between the two core types of integrals in mathematics:
- Indefinite Integrals: These do not have specified boundaries. Solving an indefinite integral results in a completely new mathematical function (the antiderivative) plus an unknown constant of integration, typically denoted as \( + C \).
- Definite Integrals: These feature specific upper and lower limits (intervals). The calculation process evaluates the function strictly between these two boundary points, resulting in a concrete numerical value (the area) rather than an algebraic expression.
Real-World Applications of Integration
Definite integrals extend far beyond theoretical mathematics. In physics, integrating a velocity function over a specific time period yields the total exact distance traveled. In economics, integrals are used to determine consumer and producer surplus by finding the area between supply and demand curves. Our calculation engine utilizes advanced numerical integration techniques, such as Simpson's Rule, to rapidly approximate these complex continuous functions with extreme precision.